6÷2(1+2) = ?
さあ、あなたはこの問題を解けますか?
少し考えてみてください。
この小学生でも解けそうな計算式ですよね?
私のインスタグラムでも『6÷2(1+2)=?』の投稿をしたところ、ものすごい反響がありました。
しかし、この式は多くの数学者を巻き込んだ派閥争いになってしまいました。
今回はその経緯と結論を出したいと思います。
この問題の経緯

この論争の初まりは、台湾のfacebookコミュニティにて算数の簡単な式を投稿したところだと言われています。
その投稿にはアンケート機能も付いていて、
6÷2(1+2)の答えが「1」or「9」
といったものでした。
このアンケートには非常に多くの回答が集まり、「1」派と「9」派がちょうど半分ずつになりました。
出題者の意図としては「9」が正解、「1」が不正解という引っ掛け問題だったわけなのですが、ごれが物議を呼び「1」が正解という主張する人も多く、長い間SNSや掲示板で議論を呼んでいました。
その結果として数学者も巻き込む事態になっていきました。しかし、数学者でも「1」派と「9」派に答えが割れてしまいました。
この問題の面白いところは、計算機によっても解答がバラバラになります。
- 複数の数学者にきいても、人によって解答が異なる。
- 計算機も機種によって解答がバラバラ
- ネットの声でも、解答はバラバラ
- googleやLinuxなど主要なソフトウェアは「9」と解答
どこかでこの問題は見たが、結局答えがどちらかはっきりせず、うやむやになっている人も多いですよね?
そこで今回は結論を出したいと思います。
結論にいく前にまずは、
「9」派の主張と、「1」派の主張を整理してみよう。
6÷2(1+2)
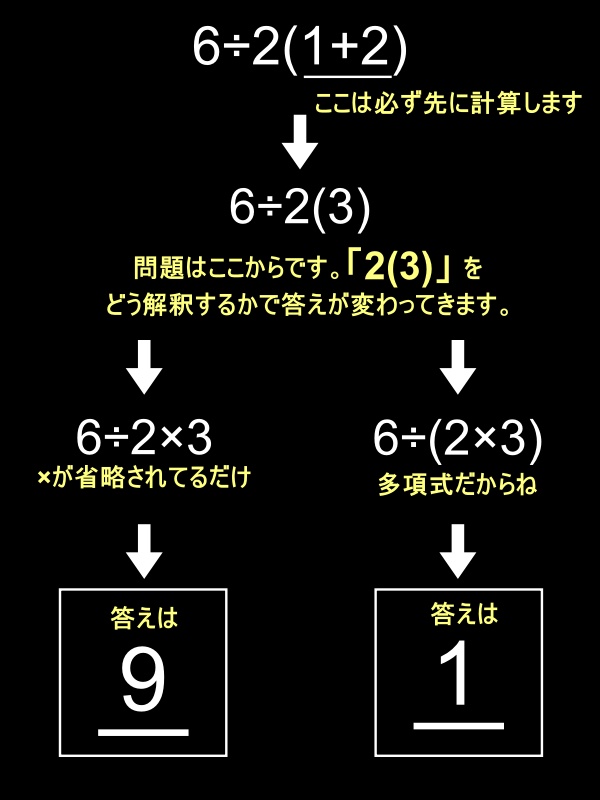
「9」派の主張
「9」は算数的な考え方になります。
四則演算にはルールがあります。
- カッコ()の中を先に計算する。
- 足し算、引き算よりも掛け算、割り算を先に計算する。
- 掛け算、割り算が共存するときは左から計算する。
これに従うと、まずカッコ()の中を先に計算すると
6÷2(1+2) = 6÷2×3
となります。次に掛け算、割り算が共存しているので左から計算すると
6÷2×3 = 3×3
となるので、答えは「9」になります。
「9」派はルールがあるんだからそれに従おうという考え方ですね。
「1」派の主張
「1」は数学的な考え方になります。
まず、以下の問題を考えてみましょう。
6a÷2a = ?
これがテストで出たら「3」の一択になりますよね?もし、この問題の答えを「3」にしなければ学校教育がよくわからないことになります。
しかし、さっきの「9」派のルール(掛け算、割り算が共存しているので左から計算する)に従うと下記のようになります。
6a÷2a = 3a^2
でも、この答えテストで書いたら不正解だと思います。このことからわかるのは2aを一つの数字として捉えているということです。
6÷2(1+2)に適応させてあげると『2(1+2)』を一つの数字として捉えるので、
6÷2(1+2)= 6÷{2×3} =1
となるわけですね。
まとめると
 6÷2(1+2)の2(1+2)をどう考えるかで異なるということです。
6÷2(1+2)の2(1+2)をどう考えるかで異なるということです。
「9」派の考え方は、2(1+2)に「×」が省略されていると考えている。
6÷2×(1+2) = 9
「1」派の考え方は、2(1+2)は一つの数字として考えている。
6÷2(1+2) = 1
GoogleやLinuxのソフトウェアが「9」と解答するのは、問題の数式を「6÷2×(1+2)」つまり、『×』を省略した式として計算するからなんですね。
では、どっちの答えが正しいのか気になりますよね?
結論
この問題の結論は定義不足になります。つまり、数式自体の書き方が間違っているということです。
2(1+2)が2×(1+2)と示しているのか、それとも一つの数字としているのかわかりませんよね?
本来、整数の式で今回のように『(』の前の『×』を省略して書くことはしないそうです
ただ、それが明文化されていないのか、あくまで通常はしないという程度だったためにここまで話が大きくなってしまったようです。
結論としては、
算数的に考えると:『9』
数学的に考えると:『1』
数式自体が間違っている!(問題の出し方が悪い)ということでした。
ちなみにGoogleに答えを出してもらうと「9」になります。

ちゃんと画像を見るとGoogleは
(6÷2)×(1+2) = 9
という風に解釈しているんですね。
それではまた。
みんてぃあ














